How to Improve the Signal-to-noise Ratio of X-ray CT Images
People often describe their X-ray CT (Computed Tomography) images as “grainy” or “noisy,” or just plain “bad” and ask me how they can make them “better.” In most cases, what they are dealing with is a low signal-to-noise ratio (low SNR), and this is what’s causing all kinds of problems. Our goal in CT image analysis is usually to study the internal structure of a sample by differentiating materials either by eye or by image segmentation based on their gray levels. Low SNR makes this differentiation difficult. To keep it simple, I’m going to call an image that makes it easier for us to differentiate materials of interest a better image.
Read: What is micro-CT?
So, in an attempt to help you make your CT images better, I am going to address the following questions in this article:
- What is SNR?
- Why is SNR important?
- What are the sources of noise?
- How can we improve SNR?
- What about denoising?
Before we dive into the SNR discussion, let’s consider general X-ray CT image quality. Assuming the sample fits in the field of view (FOV) and has good density contrast, here are the desired attributes we strive for:
- High SNR
- High resolution
- Short scan time
These are in a trade-off relationship. As you read on, keep in mind the general rule: you get to pick two but can’t have all three at the same time.
1. What is SNR?
SNR stands for a signal-to-noise ratio and is defined as [mean signal value / standard deviation]. The signal value is the gray value in CT images, which is related to the number of X-ray photons converted into a signal by the detector. The standard deviation is the fluctuation of this signal. Therefore, you can roughly interpret SNR as [meaningful X-ray signal count / noise count].
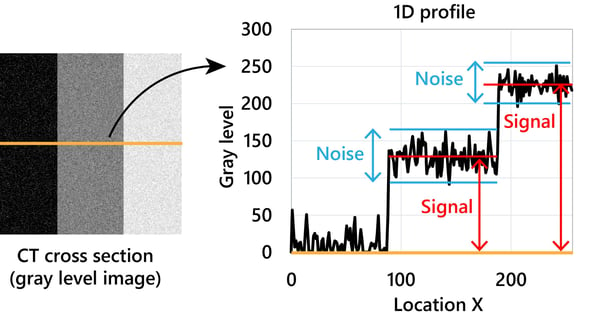
A low-SNR image has the noise level close to the signal level. This makes the image “noisy,” “grainy,” or “bad.” We want to increase the SNR to make the image better. We can do so either by increasing the X-ray signal count or reducing the noise.
As I mentioned earlier, our goal in CT image analysis is usually to study the internal structure of a sample by distinguishing different materials either by eye or by image segmentation. To distinguish two materials, they need to show significantly different gray levels. In other words, we need good contrast between the two materials. Given the same SNR, a higher contrast value provides better distinction between the two materials, as shown in the example below. Increasing the contrast helps to make images better.
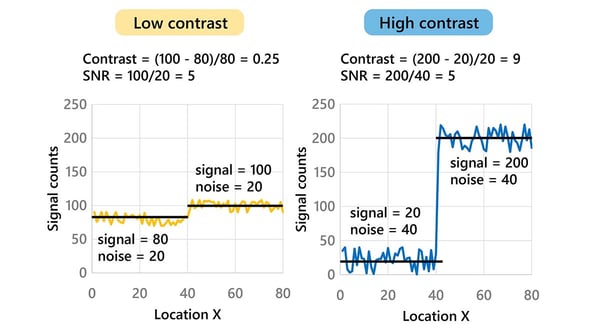
2. Why is SNR important?
Here is a comparison of low- and high-SNR images and their segmentation results generated by simple binarization. When the SNR is low, it isn't easy to achieve clean segmentation. The low SNR segmentation result has background (black) mixed in the object (white) and vice versa. By contrast, the high-SNR image provides clean segmentation with well-defined edges. This is why SNR is important.

3. What are the sources of noise?
A high-level noise reduces SNR, so noise is bad. But where is it coming from? There are two types of noise: fixed-pattern noise and random noise. Fixed-pattern noise can come from spatial non-uniformity of the incident X-ray intensity, detector sensitivity, background level, etc. These are reproducible, so we can correct them. Random noise is what usually decreases SNR. It comes from random fluctuation of the X-ray photon count from the source (shot noise or Poisson noise) and the noise the detector system introduces. Most X-ray CT scanners use an analog, non-photon counting detector, such as a CCD, sCMOS, or FPD. These detectors have dark current or thermal read-out noise, as well as noise that arises from the scintillator, analog-to-digital converter, etc. (If you are interested in learning more about detector characteristics, especially about CCDs and sCMOSs, Oxford Instruments Andor has a great learning center.)
4. How can we improve SNR?
Since SNR is a signal divided by noise, we can directly improve it by either increasing the signal or reducing the noise. Also, the SNR can be improved by accumulating the total signal count. This is because the shot noise is proportional to the square root of the photon counts. When the total count is M, the shot-noise-based SNR is proportional to M/√M = √M. This means that, given all other conditions the same, spending more time to accumulate more photons (increasing M) improves SNR.
However, before concluding that we have no other choice but to run a 30-hour scan, let’s check the basics:
Maximize the X-ray intensity
To maximize the X-ray intensity, you can set the X-ray source applied voltage, filament current, and filter to maximize the
X-ray intensity within the capacity of the source, acceptable focus size, optimized voltage, and filter combination for the best contrast. (How you balance all those parameters is enough for another article.)
Calibrate the detector
Make sure to calibrate the detector to minimize both the fixed-pattern and random noise. If you are using a CCD or sCMOS, make sure the detector is cooled to the manufacture’s recommended temperature to minimize thermal noise, and use an optimum read-out frequency. For a CCD or sCMOS, higher temperature increases the thermal noise (dark current), and a higher read-out frequency increases the read-out noise.
Optimize sample size (if you can)
Using a FOV significantly smaller than the overall sample size increases the noise level. The part of the sample outside of the FOV is still in the X-ray beam path and absorbs X-ray photons. Reconstructing just the FOV of interest while ignoring absorption by the surrounding volume increases the noise level in the CT image. A larger sample absorbs more X-ray photons and also reduces the overall X-ray photon count. So, if possible, match the sample size to the FOV. It helps improve SNR.
Reality check
If the signal is very low, for whatever reason, do a reality check. Collect just one projection image with a relatively long exposure time: 30 seconds, for example. If you see no meaningful contrast in the projection, it means the signal is too low and too close to the background level. In this case, it is probably wise to change the experimental settings rather than committing to a 300-hour scan. The X-ray energy or power might need to be higher, or the sample might need to be smaller. Either way, the signal needs to be significantly above the background level.
Now, you have done all these things, yet your image is noisy. It is time to start thinking about a longer scan. However, increasing the scan time is not the only way to accumulate/collect more photons.
You can do any of the following:
- Increase the total scan time
- Shorten the source to image/detector distance (SID)
- Bin pixels
Let’s take a look at some examples.
Increase the total scan time
Spending a long time always helps, as you can see in the example below. This is an example of increasing the number of frames. You can also increase the exposure time. Because the read-out noise increases with the number of frames you read-out, it is better to increase the exposure time first until the maximum X-ray count reaches about 80-90% of the maximum count the detector can handle (65536 counts for most detectors), then increase the number of frames next.

(Note: SNR was calculated by ImageJ plugin "SNR" written by Daniel Sage and converted to signal/noise from the original value in decibels.)
It might not be as obvious as increasing the exposure time or the number of frames, but increasing the number of projections also helps. A CT image is reconstructed from a set of 2D projections. The more projections (more X-ray counts) you put into each reconstructed voxel, the better SNR becomes. The example below is a comparison of 900 vs. 1800 projections.

(Note: The SNR was estimated as [mean gray value / standard deviation] of the water area.)
By the way, as you might have noticed in this example, the improvement of SNR is not linear to the increase of scan time. Increasing the scan time improves SNR mainly because most of the noise is shot noise, which is proportional to the square root of the signal count. The greater the total count is, the higher the SNR. However, an N-times-longer scan only means √N-times-better SNR. You might have also noticed that 7.2 times √2 is 10.2, not 9.2. The improvement of the SNR is not exactly × √N due to the influence of the background level, noise increase caused by the repeated read-out process, and the limited number of voxels used to calculate the SNR.
Shorten the source to image/detector distance (SID/SDD)
This is a technique people seem to forget sometimes. Shortening the SID/SDD increases the solid angle of X-rays the detector can capture, so the total photon count increases. The example below shows two steps of SNR improvement: increasing the scan time and shortening SID. The FOV and voxel size were kept the same.
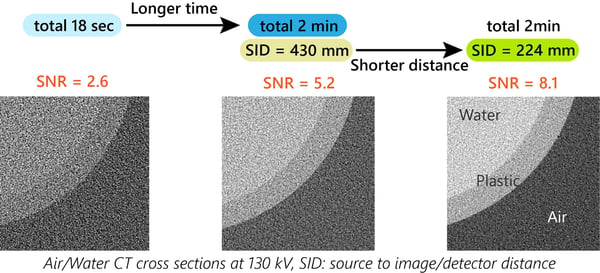
(Note: The SNR was estimated as [mean gray value / standard deviation] of the water area.)
Bin pixels
Binning pixels increases the total signal count per pixel and improves SNR at the expense of resolution. Although resolution is sacrificed, if you need to scan fast for in-situ and other time-resolved experiments, binning can be a lifesaver. The example below shows the effect of binning on SNR.
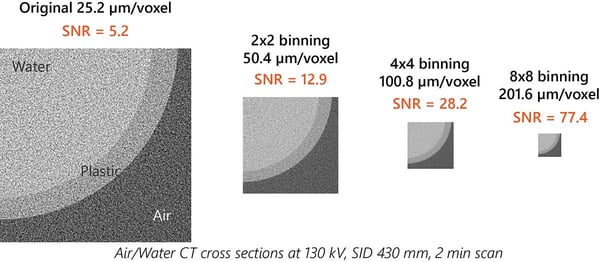
(Note: SNR was calculated as [mean gray value / standard deviation] of the water area.)
5. What about denoising?
You can improve SNR by applying image processing after the fact. There are two categories for this process. One is applying denoising filters, such as Gaussian or median filters. The other method is noise reduction by machine learning or deep learning.
The idea behind denoising filters is to average local gray values or “smooth it out” to reduce noise. These filters help improve SNR, but they usually smooth and blur the interface between materials (edges) at the same time. Of the commonly used filters, the median filter is relatively good at preserving edges. The non-local mean (NLM) filter is even better at preserving edges, although the calculation is slower than that of traditional filters. The other approach is to use deep learning. There are many different approaches. We are seeing successful results using the Noise2Noise method by Lehtinen. (If you prefer a video, you can watch Lehtinen's lecture on this method.) Some of the more recently developed ones work great, but they are, in general, even more computationally taxing.
Watch: Processing Images using ImageJ to learn more about denoising filters
This is probably a good time to remind ourselves why we need to reduce the noise to begin with. We want to distinguish different materials in CT images by their gray levels. If you can look at the image and identify these materials based on their gray levels, that is good. But if you can’t see it, no fancy denoising or segmentation algorithm is going to magically make some feature appear. In this case, the experiment needs to be adjusted until you can see something.
I have addressed the five questions as I promised at the beginning. I hope you now have an idea about how to make your CT images better. Before you go, here is one more thing to think about.
An alternative approach - Machine / deep learning segmentation
Even after taking all the measures mentioned here, what often frustrates us still is this situation: We see that something is there, but segmentation doesn’t bring it out in the way we want because the SNR is not quite high enough. Smoothing filters can reduce this problem somewhat, but you might lose the edges. There is a better way. If you can see it, you can train a machine-learning or deep-learning network to see it the same way you do and obtain clean segmentation using the unprocessed, still-a-bit-noisy image.
We previously saw that a low-SNR image could give you noisy segmentation. Let’s take that same low-SNR image and segment it in two different ways. You can apply the median filter then threshold it (on the right in the figure below) or you can segment the original image using machine learning (on the left in the figure below). You can see that machine learning can segment the original low-SNR image with no problem. Machine learning is excellent at ignoring the noise and can segment most images based on the average gray level. When additional parameters such as shape, size, and location of a certain material need to be considered, you can use deep learning.
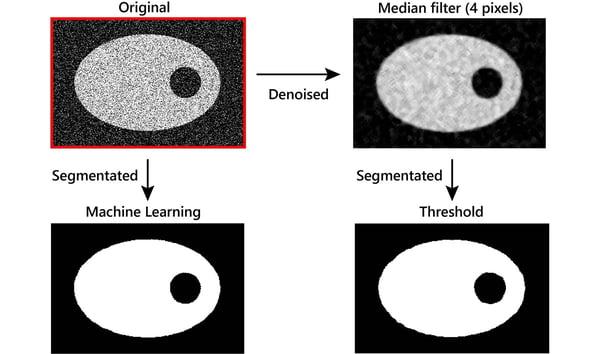
When threshold-based segmentation doesn't work well because of low SNR, consider using machine-learning or
deep-learning segmentation. These techniques are incredibly robust against random noise. I prefer this method over denoising filters because if you use the original image and deep-learning segmentation, you can easily overlay the original and the segmentation results and correct any biases you see.
Low SNR is not a unique challenge; it is a universal problem in data collection; therefore, we might see more innovative ways to overcome it in the future. I definitely look forward to them. But in the meantime, I will continue to optimize scanning conditions, run long scans, and play with deep-learning segmentation.
I hope you now have a plan and are ready to get back to the lab.
If you want to see us playing with and optimizing scan conditions to balance the SNR and resolution, you might like this virtual workshop on high-resolution CT measurement techniques. If you have any questions, click the "TALK TO AN EXPERT" button at the top of this page and book a meeting with one of our experts or email us at imaging@rigaku.com.
(This article was published originally on LinkedIn. The article has been edited, and extra resource links have been added.)
You might also like: Processing Images Using ImageJ (Virtual workshop on denoising and sharpening filters)


